![[UCR]](../../img/ecci02.gif)
![[/\]](../../img/top.gif) |
|
Escuela de Ciencias de la Computación e Informática |
![[UCR]](../../img/ecci02.gif)
|
|
![[<=]](../../img/back.gif)
![[home]](../../img/home.gif)
|
![[<>]](../../img/index.gif)
|
![[\/]](../../img/bottom.gif)
![[=>]](../../img/next.gif)
|
|
Adolfo Di Mare
|
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
Discutimos cómo es el funcionamiento y la
implementación de la clase de
plantillas C++
Tree, que puede ser usada para programar algoritmos
recursivos que trabajan en jerarquías. Esta clase
genérica es bastante general y subsume la mayoría de
las abstracciones descritas en los libros de texto.
|
We discuss how the workings and implementation of the
Tree template class which can be used to program
recursive algorithms that work in hierarchies. This generic
abstraction is quite general and subsumes most tree abstractions
described in text books. |
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
La construcción de programas por partes, usando
módulos, se
facilita mucho cuando se usan clases. Muchas clases existen porque
corresponden a objetos concretos, como ocurre con las clases
"Persona" o "Número Complejo"; a éstos
módulos
básicos
podemos llamarles
Clases elementales. Hay otras clases, las que
llamamos clases Contenedoras, que sirven para
almacenar a otros objetos. Los
contenedores más importantes son tres: el Vector o
Arreglo, la Lista y el Arbol. Existen otros contenedores, como
"Heap.pas",
"Poly.pas",
"Matriz.c++", etc, pero
la mayoría de las estructuras de datos importantes se
obtienen al combinar vectores,
listas
y
árboles. En lenguajes potentes
como C++ es posible crear los contenedores usando
plantillas, que es el camino que se ha tomado para realiar este trabajo.
Indiscutiblemente, el más importante de todos los contenedores es el vector, que es una construcción sintáctica básica de la mayoría de los lenguajes de programación. La Lista le sigue en orden de importancia, pues generalmente está implementada como una estructura dinámica que le evita al programador definir de antemano la capacidad máxima que necesitará, lo que facilita la escritura de programas. Es tan importante la lista que hay lenguajes especializados en su uso, como por ejemplo Lisp o Scheme.
En comparación a los otros contenedores, los árboles se usan relativamente poco, pues la mayor parte de los programas no necesitan manejar estructuras jerárquicas recursivas. De hecho, la biblioteca STL de C++ está compuesta de contenedores "lineales", pues todos son secuencias que tienen algunas cualidades adicionales [Brey-2000]; lo mismo ocurre con la biblioteca de componentes que construyó Microsoft para su plataforma .NET. Además, con las listas es posible implementar árboles, por lo que en aquellas ocasiones en que una jerárquicas recursiva es la solución, muchos programadores escogerán escribir su programa de árboles directamente, o utilizan árboles binarios, cuyos algoritmos se pueden encontrar en la mayoría de libros de texto sobre estructuras de datos [AHU-84]. Aunque el árbol no es tan importante como la lista, es conveniente estudiarlo por lo menos por las siguientes razones:
Tree", que permite usar las clases sin necesidad de
conocer la
estructura interna del árbol, ni la de sus nodos, que
es lo que ocurre con otras implementaciones
[BD-96]. Por eso, en las especificaciones de
las operaciones nunca es necesario mencionar el concepto de
"Nodo", que está presente en casi todos los árboles
descritos en los libros de texto; el uso de estas clases permite
la
separación de funciones que es requisito necesario
para aplicar con éxito la abstracción al construir
programas.Tree" no hace falta manejar punteros, lo que resulta
en una clase muy simple, que consiste únicamente del tipo
"Tree" junto con sus
operaciones.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
Antes de implementar la clase "Tree" es necesario
definir qué es un árbol. Los árboles son
grafos, pues están compuestos de nodos y aristas que los
unen. Para definir matemáticamente un árbol es
necesario definir primero el concepto de Camino,
que es una secuencia de aristas que conectan nodos, en que la
arista siguiente en el camino comienza en el nodo en que termina
la arista anterior. Un Circuito es un camino en
el que el primer y último nodo son el mismo, y un
Circuito simple es un circuito en que cada nodo
aparece sólo una vez. Se dice que el grafo es
Conectado si siempre existe un camino entre
cualesquiera 2 nodos del grafo. Con base a estos conceptos son
equivalente las siguientes definiciones matemáticas del
árbol "T"
[Even-79]:
Todas estas definiciones son escuetas, correctas y completas pero, paradójicamente, no hablan de las propiedadas principales de los árboles, por lo menos desde el punto de vista del programador, pues no mencionan que un árbol en una jerarquía encabezada por su raíz. De hecho, en estos árboles matemáticos cualquier nodo podría fungir como nodo raíz. Estos hechos son muestra de que el concepto de árbol no es fácil de definir, pues tiene muchos posibles significados (¿qué es un árbol binario?).
Una forma de definir qué es un árbol es mostrar cómo está hecho. En los libros de texto lo usual es definir un árbol como un conjunto finito de elementos o nodos organizados de acuerdo a las siguientes propiedades:
T.Empty()].T.Root()]
del que todos los demás nodos son descendientes
[T.Child(i)].T.Father()].T.Sibling(i)].Is_Leaf(T)].Depth(T)].Height(T)].T.Child(i)].n"
aunque no tenga hijos anteriores o posteriores.Las últimas 2 condiciones son necesarias para que la definición de lo que es un árbol sea completa, pues al eliminarlas ocurre que los dos árboles binarios que tengan uno un hijo izquierdo y otro el mismo hijo, pero a la derecha, serían iguales.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
T = A A
/|\ /
B C D B
/ \ \
L M C
/ \
L D
\
M
|
|
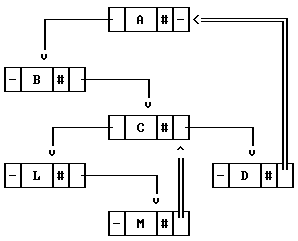
Un truco bien conocido es el de usar un árbol binario para
representar los valores de un
árbol "n"-ario, como se muestra en la
Figura 1. La forma de hacerlo es
bastante simple, pues ambos árboles tienen la misma
raíz. En el árbol binario, el hijo izquierdo siempre
es el primer hijo del
árbol "n"-ario, mientras que los hijos
derechos del árbol binario son los hermanos del hijo
izquierdo. Como sobra un puntero a la derecha en el nodo del
último hijo (en los nodos "D" y
"M"), queda muy conveniente poner ahí un
puntero al padre, lo que se ha enfatizado en la figura al usar
doble línea. Todos los punteros en el árbol se usan,
y únicamente el nodo raíz tiene su puntero derecho
nulo, pues en un árbol sólo la raíz no tiene
nodo padre. Esta estructura de datos es muy compacta y
eficiente
[HS-92].
El inconveniente de estos árboles llamados
"Hijo-izquierdo Hermano Derecho" es que para llegar al hijo
número "n" hay que visitar antes a todos los
hijos anteriores, mientras que en el árbol implementado con
un vector de punteros a los hijos esta operación es
inmediata, pues en un vector la cantidad de tiempo para llegar a
cualquiera de sus elementos siempre es la misma. La ventaja de los
árboles hijo+hermano es que no desperdician espacio en
punteros nulos, y además sirven para representar de manera
natural cualquier
árbol "n"-ario, pues no tienen la
limitación de un máximo de hijos por nodo (siempre y
cuando haya
memoria dinámica suficiente). Por eso, en muchas
ocasiones es preferible usar árboles hijo+hermano, pues no
requieren del
programador cliente grandes cuidados para evitar sobrepasar
el límite de número de hijos.
Al implementar los árboles hijo+hermano surgen algunas dificultades que hay que mencionar. Lo primero es que se hace necesario incluir en el nodo algún marcador que permita diferenciar si un puntero derecho apunta a otro hermano, o si más bien ahí está el puntero al nodo padre que tiene el último hermano. Existen varios trucos de programación para lograr esta diferenciación entre los que se pueden destacar dos. El primero, y talvez el menos complicado, es esconder en el puntero final un "bit" que indique si ese puntero es o no un puntero al padre, usando un truco de programación similar al expuesto en [DiM-2000b]. La razón por la que aquí no se usa el truco del "bit escondido" es que es difícil de explicar a estudiantes novatos, y además se puede lograr el mismo efecto con la otra alternativa descrita más adelante.
// (m_n_child < 0) ==> Es el puntero al padre
class Tree_Node {
private:
value_type m_data;
unsigned m_refCount;
int m_n_child; // incrementado en int(1)
Tree_Node * m_left_child;
Tree_Node * m_right_brother;
}; // Tree_Node
|
m_n_child"
para registrar cuál es el número de hijo entre todos
los hijos de un mismo padre, que se obtiene con el método
"Child_Number()"; ahí se puede también
indicar si un nodo es el último en la lista de hijos de su
padre, almacenando un valor negativo en el campo
"m_n_child".
El campo "m_refCount" sirve para mantener un contador de referencias, lo que facilita mucho el trabajo con árboles y sus sub-árboles.
Como en C++ todos los índices comienzan en cero
"0" (no como en Pascal o Fortran, en donde comienzan
en uno "1") en muchos casos existirá el hijo
número cero
(de hecho, el hijo izquierdo en un árbol binario es
precisamente "Child(0)"). Sin embargo, el cero tiene
la particularidad de que es el único número que es
igual a su negativo
"0 == -0", por lo que el campo
"m_n_child" no podría contener un
número negativo para el único hijo número
cero. Por eso, en la implementación se almacena el valor
"-n-1" o el valor
"+n+1" en el campo "m_n_child"
dependiendo de si el nodo es o no el último en la lista de
hijos del nodo padre.
En la discusión que sigue su usa la implementación
de listas de la clase árbol, llamada
"TL::Tree"; también se realizó la
implementación
"TV::Tree" usando un vector de punteros, que es
funcionalmente equivalenta a
"TL::Tree", pero cuyas cualidades de rendimiento no son
discutidas acá por razones de espacio.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
En las secciones anteriores la mayor parte de la discusión se hizo desde la óptica de la implementación, por lo que fue necesario usar la palabra "Nodo" muchas veces. Como ocurre con las listas de Lisp, es posible especificar el árbol sin usar el concepto de "Nodo", usando más bien sub-árboles, así como la listas Lisp están definidas en término de sus sub-listas. Por analogía con Lisp, un sub-árbol es una parte de un árbol.
Lo más simple muchas veces es suficiente; afortunadamente, basta definir un sub-árbol como un objeto que contiene una referencia hacia el valor almacenado en la jerarquía que representa la raíz del sub-árbol. La diferencia principal entre árboles y sub-árboles es que los primeros nunca tendrán en su raíz una indicación de quien es su padre, pues por definición la raíz un árbol no tiene padre alguno, mientras que sí puede ocurrir que un sub-árbol descienda de algún nodo por lo que en ese caso su raíz tendría un padre no vacío.
Una vez que se usa el concepto de "sub-árbol" en lugar del
de "nodo" se puede prescindir completamente de los nodos, porque
en lugar de manipular los nodos se puede manipular
sub-árboles cuya raíz es el "nodo" (que ya no hace
falta mencionar). Por eso, la especificación de la
operación
"Child(n)"
dice que retorna el
"n"-ésimo sub-árbol hijo, no que
retorna un nodo. Desafortunadamente, al definir los árboles
como referencias surge un problema adicional, pues hay que
mantener un control de cuántas referencias existen para
cada nodo del árbol. Habrá más de una
referencia al mismo sub-árbol si, por ejemplo, para el
mismo árbol se invoca más de una vez la
operación
"Child(n)".
Los árboles son útiles porque, además de
almacenar valores, lo hacen imponiendo una estructura que permite
luego lograr eficiencia en muchos algoritmos. Por eso, es
importante definir cuáles mecanismos existen para pasar de
un valor almacenado en el árbol a otro, y cómo se
usan esos mecanismos. Los iteradores lineales de la biblioteca STL
estándar de C++ son bien conocidos
[Mall-97],
pero a fin de cuentas no reflejan la estructura no lineal de los
árboles. Por eso, el mecanismo principal para recorrer un
árboles es visitar al padre y a sus hijos mediante la
invocación de los métodos
"Father()" y
"Child(n)".
Los árboles son
contenedores, por lo que deben incluir operaciones que
permitan
almacenar valores en el
árbol. Para ésto hay que contar por lo menos con 2
mecanismos: uno para cambiar un valor individual y el otro para
injertar
sub-árboles completos. Para agregar o cambiar un valor en
la raíz se usa
"Change_Root(d)", y para hacer lo mismo en el
"n"-ésimo hijo se usa
"Change_Child(n,d)". El método
"Graft(n,Ti)"
sirve para agregar el
sub-árbol "Ti" completo, como
"n"-ésimo hijo de "T". Los
métodos
"Erase()"
junto con
"Erase_Son(n)"
tiene el efecto inverso, pues eliminan el sub-árbol completo.
Como ocurre con cualquier
objeto, también para los árboles tiene sentido
definir sus operaciones elementales de copia, impresión,
etc. Al copiar un árbol, que es una referencia, lo que se
copia es una referencia, y el resultado es una copia superficial
de valores. Por eso la operación
"Copy()"
es una copia superficial, y si se necesita una copia profunda del
árbol, hay que usar
"Copy_Deep()".
Como se usa
semántica de referencia para implementar
árboles, las operaciones para recorrer los valores
almacenados en el árbol retornan un nuevo objeto
sub-árbol cuando , como lo hace por ejemplo
"Child(n)". Esas referencias no son los valores almacenados del árbol y en consecuencia al intercambiarlas, mediante el método
"Swap()"
o al copiarlas, mediante el método
"Copy()", no se modifica los valores almacenados en el
árbol. Para modificar los valores almacenados es necesario
usar los métodos que realizan esa función, como lo
son
"Change_Root(d)",
"Change_Child(n,d)"
o
"Graft(n,Ti)".
Por eso, si se usa
"Swap()" para intercambiar 2 árboles obtenidos
mediante invocaciones a
"Child(n)"
no se logrará cambiar los valores de los árboles
originales.
/** Convierte a "T" en su sub-árbol espejo, en el que recursivamente los hijos
quedan en orden inverso del orden en el que aparecían originalmente en "T"
a a
/|\ /|\
/ / \ \ / / \ \
b c d e e d c b
/|\ /|\ /|\ /|\
f g h i j k k j i h g f
/ \ / \
l m m l
/ \ / \
n o o n
*/
void Mirror( Tree& T ) {
if ( T.Empty() ) {
return; // se sale si el árbol está vacío
}
Tree Child = T.Leftmost();
while ( ! Child.Empty() ) { // recursión para cambiar a todos los hijos
Mirror( Child );
Child = Child.Right_Sibling();
}
unsigned N = T.Rightmost_N();
Tree Ti, Tn_i; // [0] [1] [2] [3] [4] N == 4
unsigned i, Mid = (N+1) / 2; // i i < 2 == Mid ==> 2 == 4/2 == 5/2
for (i=0; i<Mid; ++i) { // Intercambia los hijos i <==> N - i
Ti = T.Child( i );
Tn_i = T.Child( N - i );
T.Graft( i, Tn_i ); assert(( Ti.Empty() ? true : Ti.Father().Empty() ));
T.Graft( N - i, Ti );
}
}
|
// [0] [1] [2] [3] [4] N == 4
unsigned i, Mid = (N+1) / 2; // i i < 2 == Mid ==> 2 == 4/2 == 5/2
for (i=0; i<Mid; ++i) { // Intercambia los hijos i <==> N - i
T.Child(i) . Swap ( T.Child( N - i );
} // \====/
|
En la parte de arriba de la
Figura 3 está la
implementación de la función
"Mirror(T)"
que funciona porque recursivamente vuelve al revés a
"T" y a todos sus
sub-árboles.
La Figura 3 es muestra de que es posible implementar algoritmos recursivos de manera natural cuando se usa el concepto de "Sub-Árbol" en lugar del de "Nodo". En ésto también ayudan las cualidades sintácticas del lenguaje C++, cuyos mecanismos de herencia y sobrecarga de nombres permiten escribir con naturalidad los algoritmos, sin sacrificar el ocultamiento de datos.
El algoritmo "Mirror(T)" implementado en la
Figura 3 también sirve para ver
que es muy cómodo usar
sub-árboles pues, para simplificar la
implementación, dentro del ciclo
"for" se usan los 2
sub-árboles temporales "Ti" y
"Tn_i". Al principio del ciclo
"for" el resultado de la
asignación
"Ti = T.Child(i)"
es hacer que el valor de "Ti" sea un
sub-árbol cuyos valores están almacenados como
sub-árbol de "T", con lo que efectivamente
"T" y "Ti" comparten sus valores
almacenados (esto quiere decir que si se ejecutara la
operación
"Ti.Change_Root(d)" cambiaría
tanto el valor de "Ti" como el de
"T"). Después de la ejecución de la
operación
"T.Graft(i,Tn_i)"
ya no hay valores comunes entre "T" y
"Ti", pero sí ocurre que
"Ti" mantiene los valores que fueron
parte de "T". Por eso, pese a que la operación
"T.Graft(i,Tn_i)" elimina
"Ti" como
sub-árbol de "T", en
"Ti" quedan los valores que luego
son intalados como el hijo número
"N-i" gracias la la última
operación del ciclo, operación
"T.Graft(N-i,Ti)"
Para intercambiar los sub-árboles de la
posición "i" a "N-i" en
"Mirror(T)" es necesario usar
"Graft(n,Ti)" pues si se usara un simple
"Swap()", como está en la parte de abajo de la
Figura 3, el resultado sería
intercambiar las nuevas referencias a los hijos de
"T" que
"Child(n)" retorna, pero eso no cambia los valores
almacenados en "T". En otras palabras, el efecto de
esa invocación a
"Swap()" sería dejar el árbol
"T" con su valor original, e intercambiar las
referencias que contienen los
sub-árboles temporales que las 2 invocaciones a
"Child()" producirían, lo que no tiene efecto
en el valor de "T".
Después de que un estudiante logra comprender por
qué es necesario usar
"Graft(n,Ti)" en lugar del simple
"Swap()", ya no tendrá dificultad en saber
cómo funcionan los lenguajes que usan la semántica
de referencia como mecanismo fundamental para manipulación
de datos, como ocurre en los lenguajes Java y C#.
Después de analizar la
implementación del algoritmo
"Mirror(T)" en la
Figura 3 es natural deducir la
especificación de cada una de las
operaciones de la clase "Tree". La clase
"TL::Tree" facilita la escritura de algoritmos
recursivos que manipulan la
estructura del árbol, sin importar cuál es su
contenido, porque el
acoplamiento entre los
valores almacenados y el contenedor es muy bajo.
class Bin_Tree {
Node * m_root;
public:
struct Node {
Node *m_left, *m_right;
value_type m_data;
};
friend void Print0( Node * );
void Print() { Print0(m_root); }
};
|
// Print0() trabaja con nodos
// - No trabaja con el árbol
void Print0( Bin_Tree::Node *p) {
if (p != 0) {
Print0( p->m_left );
cout << p->m_data << ' ';
Print0( p->m_right );
}
}
|
Tradicionalmente, los algoritmos recursivos que trabajan con
árboles tienen que ser implementados en 2 partes, en donde
hay un procedimiento externo que recibe parámetros de tipo
"árbol" y luego invoca un procedimiento recursivo que
realmente realiza el trabajo, y como argumento se le envía
un puntero al nodo raíz del árbol, como se muestra
en
Figura 4 con la función
"Print0()" y el método
"Bin_Tree::Print()". Esta forma de proceder no es
conveniente porque induce al programador cliente a usar los campos
privados del objeto, y así violentar el
ocultamiento de datos que es el mecanismo que se usa para
evitarle al programador cliente conocer cómo está
implementado un
módulo de
programación. La abstracción definida aquí
permite implementar la función
"Print()" en término de
sub-árboles, y sin usar una rutina intermedia como
"Bin_Tree::Print()" cuyo único trabajo es
invocar al procedimiento recursivo que realiza el trabajo. Por
eso, la gran ventaja de esta especificación del
árbol es que permite manipular información
organizada jerárquicamente, pero evita el uso de punteros,
que tanta dificultad representan para la mayor parte de los
programadores.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
La cantidad de operaciones que tiene la clase
"Tree",
es muy grande, pues incluye todas las operaciones que deben ser
incluidas. Sin embargo, en la mente de las personas no son todas
las operaciones las que identifican a la una
clase.
\ |___ | | ^ ^ |
La Figura 5 es una silla. No es una
silla bonita, pero ti tiene su sentadera, sus
paticas y el
respaldar. Este dibujo es una
abstracción del concepto silla, pues
"abstraer" significa "Separar las cualidades de un objeto
para considerarlas aisladamente o para considerar el mismo objeto
en su pura esencia o noción". Cuando se habla de una
pila en programación, el programador usuario entiende que
se habla de un contenedor que tiene 2 operaciones
principalísimas: "Push()" y
"Pop()". En la biblioteca STL las pilas son parte de
todos los contenedores, porque casi todos tienen las operaciones
"push_front()"
y
"pop_front()".
De hecho, la plantilla
"stack<>"
funciona porque estas operaciones están bien definidas para
los otros contenedores. Lo mismo ocurre con las colas y sus
operaciones "Enqueue()" y "Dequeue()".
Por eso es importante definir cuáles son las operaciones
"principalísimas" para la clase
"Tree".
Child(n)
|
Acceso al "n"-ésimo hijo |
TL
|
TV
|
operator * ()
|
Acceso al valor almacenado en la raíz |
TL
|
TV
|
Change_Root(d)
|
Sustituye por "d" el valor almacenado en la raíz |
TL
|
TV
|
Erase()
|
Elimina el árbol y sus descendientes |
TL
|
TV
|
Father()
|
Acceso al padre |
TL
|
TV
|
Graft(n,Ti)
|
Injerta "Ti" como "n"-ésimo hijo |
TL
|
TV
|
En la Figura 6 están las
operaciones principales de un árbol. En muchas ocasiones se
usa un concepto de árbol que no incluye las operaciones
"Graft(n,Ti)"
y
"Father()"
porque muchas veces las implementaciones sólo tiene un
puntero a los hijos. Puede ocurrir también que se hable de
"Erase_Son(n)"
en lugar de
"Erase()"
para es frecuente no incluir el puntero al padre que hay que usar
al implementar "Erase()". Aunque la operación
más compleja es
"Graft(n,Ti)",
la más importante es
"Child(n)", que es la que permite llegar a los hijos
desde el padre, pues casi siempre se usa un árbol porque se
necesita este tipo de acceso. Desde el punto de vista más
general, con los árboles ocurre algo similar a lo que
ocurre en las listas, en las que la operación principal es
avanzar hacia el siguiente nodo invocando
"List::Next()".
¿Tiene sentido usar árboles que no tengan alguna de
las operaciones de la
Figura 6?
Esta es una pregunta teórica, pues en la práctica
los árboles son "nodos" que almacenan un valor y
que están "conectados" a sus hijos derecho e
izquierdo, pues casi siempre lo que se usa es un árbol
binario.
Siendo así las cosas, y debido a que no es usual incluir un
puntero al padre, que es lo que permite implementar con relativa
eficiencia la operación
"Graft()",
se puede decir que la abstracción aquí descrita no
concuerda con lo que se usa en muchos libros de texto. Pero si es
válido alzar la conjetura de que, junto con el desarrollo
de la tecnología y el conocimiento, poco a poco esta
abstracción del árbol será más
utilizada.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
La especificación completa de la clase fue extraída del código fuente usando el sistema de documentación Doxygen [VANH-2004].
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
Talvez la exposición en este artículo debiera haber comenzado por lo más abstracto, para llegar al final a lo más concreto. Sin embargo, los programadores aprendemos como los niños: de lo concreto a lo abstracto. Por eso, con frecuencia partimos de una implementación para luego obtener la abstracción que le corresponde. El último paso es definir el trabajo realizado, escribiendo la documentación de la especificación (en lo que afortunadamente ayuda mucho contar con herramientas como Doxygen que extraen las especificaciones del código fuente). Después de todo, la razón para usar abstracción es construir programas, lo justifica el enfoque aquí usado.
En general la parte más compleja en la implementación es la manipulación de punteros, pues un pequeño descuido puede resultar en un puntero roto, que en general tiene efectos impredecibles en el programa. Precisamente por lo difícil que es manipular punteros se justifica usar clases y módulos, que permiten encapsular el uso de punteros en una sección aparte de la implementación, para facilitar la depuración independientemente del resto del programa.
Mantener las cuentas de referencia en el campo "m_refCount" es una tarea difícil, pues es muy fácil perder la cuenta cuando se construyen y destruyen objetos. La ventaja de usar cuentas de referencia es que facilita mucho la
copia de objetos, pues el método "Copy()" sólo tiene que copiar un puntero y aumentar un contador. Debido a la complejidad de estas 2 implementaciones, definitivamente para un estudiantes es provecho conocer cómo se
manipulan por doquier las cuentas de referencia "m_refCount", cuyo uso contribuye a posponer la destrucción de objetos hasta que todavía
están en uso.
Respecto del uso de cuentas de referencia cabe hacer una
digresión importante. Los programadores C++ con frecuencia
alimentan el mito de que C++ es un lenguaje más
"rápido" o "eficiente" que otros lenguajes más
modernos, como lo son Java o C#. Sin embargo, si los
árboles acá descritos hubieran sido implementados en
alguno de esos 2 lenguajes, seguramente tendrían un mejor
desempeño que la versión C++, pues Java y C# usan un
recolector de basura que funciona cuando se requiere, o sea,
que se activa cuando se agota la
memoria dinámica. Debido a que los computadores ahora
tienen cantidades enormes de memoria, ese evento es relativamente
raro, por lo que la versión C++ requeriría
más tiempo de ejecución porque cada ves que se hace
una copia en C++ es necesario también incrementar o decrementar los contadores de referencia "m_refCount", lo que no ocurre en las implementaciones Java o C#. En otras palabras, la estrategia C++ para recuperar memoria dinámica
es muy avara
(greedy), y esa política no siempre da buenos
resultados: C++ cuenta los centavos mientras que los otros
sólo se ocupan de los millones.
La especificación de
"Copy()" y de las otras operaciones de
copiado retorna una referencia "Tree&" en
lugar de un nuevo objeto de tipo "Tree" por razones
puramente de eficiencia, pues en el contexto en que esas
operaciones se pueden usar no existe el problema de que el uso de
la referencia cause un efecto colateral indeseado. Si en la
implementación no fuera necesario usar el contador de referencias "m_refCount", estos métodos retornarían un nuevo objeto "Tree" por eso es más sencillo. Este es un ejemplo en donde la búsqueda
de la eficiencia en la implementación tiene un impacto en la especificación.
Definitivamente, en ambas implementaciones la operación
más compleja es
"Graft()",
pues la manipulación de punteros que requiere es muy
intrincada. Esta operación es el centro de la
implementación. Como generalmente es más
fácil manejar vectores que punteros, es natural que la
implementación de
"TV::Graft()"
sea mucha más sencilla que la de
"TL::Graft()", pues es la versión de listas es
necesario usar el método privado intermedio
"Erase_Son_Prev()" que tiene una estructura de
funcionamiento
muy compleja.
Es curioso, pero la función
"Mirror()" de la
Figura 3 no es idempotente, pues al
aplicarla 2 veces consecutivas no siempre se obtiene el mismo
árbol original, pues la rotación de los hijos se
hace intercambiando el hijo "int(0)" con el
número
"Rightmost_N()",
por lo que si hay 2 hijos, "[1+9]" por ejemplo, al
sacar el espejo la primera vez quedarán numerados
"[0+8]", y luego quedarán numerados
"[0+8]" de nuevo, y se perderá la
numeración original "[1+9]".
El programa
"Tree_test.cpp" puede ser muy útil para determinar cuál es el funcionamiento de cada operación, pues en muchos casos se usar la macro
"assert()" para verificar el resultado correcto de la
ejecución de cada operación.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
Hasta hace pocos años en los cursos intermedios de programación se usaban las listas para mostrar los conceptos de abstracción y especificación para los construcción de programas por módulos. Debido a que ahora ya existen muchas bibliotecas completas de contenedores lineales [Mall-97] , conviene usar el objeto contenedor árbol como instrumento didáctico para enseñar técnicas avanzadas de programación. La implementación que aquí se presenta es un paso en esa dirección.
La preferencia hacia C++ como lenguaje en el segundo curso de
programación se justifica por sus cualidades para
abstracción y especificación
[BLW-2001]. La aparente eficiencia de C++
no lo es tal en situaciones prácticas, en las que lenguajes
más simples como C# o Java pueden ser una mejor
alternativa; de hecho, mantener las cuentas "m_refCount" correctas aumentan la dificultad de estas 2 implementaciones en C++. Se justifica continuar usando C++ sólo en cursos en donde la eficiencia es un objetivo central, como en
Análisis de Algoritmos o Sistemas Operativos.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
La profesora Gabriela Marín contribuyó con facilidades bibliográficas. El estudiante Alejandro Di Mare hizo varias observaciones y sugerencias importantes para mejorar este trabajo.
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
[AHU-84]
|
Aho, Alfred V.; Hopcroft, John E.; Ullman, Jefrrey D.:
Data Structures and Algorithms,
Addisson Wesley Publishing Co.Computer Science Press,
1984.
|
| [BD-96] |
Berman, A. Michael
&
Duvall, Robert C.:
Thinking about binary trees in an object-oriented world,
Proceedings of the twenty-seventh SIGCSE technical symposium on Computer science education;
Philadelphia, Pennsylvania, United States;
pp 185-189;
ISBN 0-89791-757-X,
1996.
|
| [BLW-2001] | Bucci, Paolo & Long, Timothy J. & Weide, Bruce W.:
Do we really teach abstraction?,
Proceedings of the thirty-second SIGCSE technical symposium on Computer Science Education;
Charlotte, North Carolina, United States;
pp 26-30;
ISBN 1-58113-329-4,
2001.
|
| [Brey-2000] | Breymann, Ulrich:
Designing Components with the C++ STL,
ISBN 0-201-67488-2,
Pearson Education Limited, 2000.
|
| [DiM-2000a] | Di Mare, Adolfo:
C Parametrized Lists,
Revista de Ingeniería,
Universidad de Costa Rica, 2000.
http://www.di-mare.com/adolfo/p/c-list.htm
|
| [DiM-2000b] | Di Mare, Adolfo:
Como esconder datos en punteros,
Revista de Ingeniería,
Universidad de Costa Rica, 2000.
http://www.di-mare.com/adolfo/p/ptrbit.htm
|
| [DiM-2004] | Di Mare, Adolfo:
El truco del Tdef.h para la enseñanza de plantillas C++,
Reporte Técnico ECCI-2004-01(sp),
Escuela de Ciencias de la Computación e Informática,
Universidad de Costa Rica,
2004.
http://www.di-mare.com/adolfo/p/tdef.htm
|
| [Even-79] | Even, Shimon:
Graph Algorithms,
Computer Science Press,
ISBN 0-914894-21-8,
1979.
|
| [Feke-2002] | Fekete, Alan:
Teaching data structures with multiple collection class libraries,
Proceedings of the 33rd SIGCSE technical symposium on Computer science education;
Cincinnati, Kentucky;
pp 396-400;
ISBN 1-58113-473-8;
2002.
|
| [Gur-95] |
Gurwitz, Chaya:
Achieving a uniform interface for binary tree implementations,
Proceedings of the twenty-sixth SIGCSE technical symposium on Computer science education;
Nashville, Tennessee, United States;
pp 66-70;
ISBN 0-89791-693-X;
1995.
|
| [HS-82] | Horowitz, E.; Sahni, S.:
Fundamentals of Data Structures,
Computer Science Press; 1982.
|
| [KB-89] | Kumar, Ashok & Beidler, John:
Using generics modules to enhance the CS2 course,
Proceedings of the twentieth SIGCSE technical symposium on Computer science education
Louisville, Kentucky, United States;
pp 61-65;
ISSN 0097-8418;
1989.
|
| [LMc-87] | Liss, Ivan B. & McMillan,Thomas C.:
Trees - A CS2 programming project which introduces a data type using procedural and data abstraction,
Proceedings of the eighteenth SIGCSE technical symposium on Computer science education;
St. Louis, Missouri, United States;
pp 346 - 352;
ISBN 0-89791-217-9;
1987.
|
| [Mall-97] |
Mallozzi, John S.:
Binary trees á la STL,
Proceedings of the twenty-eighth SIGCSE technical symposium on Computer science education;
San Jose, California, United States;
pp 159-163;
ISSN 0097-8418;
1997.
|
| [VANH-2004] |
Van Heesch, Dimitri:
Doxygen documentation system for C++,
2004.
http://www.doxygen.org/index.html
|
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
| Archivo | Descripción | Texto | Doxygen |
|---|---|---|---|
Tree_Ex.h |
Algunas funciones de ejemplos de uso de la clase Arbol
http://www.di-mare.com/adolfo/p/TreeCpp/Tree_Ex.h
|
.txt |
.html |
Tree_L.h |
Declaraciones y definiciones para la clase Arbol [Lista]
http://www.di-mare.com/adolfo/p/TreeCpp/Tree_L.h
|
.txt |
.html |
Tree_V.h |
Declaraciones y definiciones para la clase Arbol [Vector]
http://www.di-mare.com/adolfo/p/TreeCpp/Tree_V.h
|
.txt |
.html |
Tree_test.cpp |
Tree_test.cpp ==> Ejemplos de uso de la clase Arbol
http://www.di-mare.com/adolfo/p/TreeCpp/Tree_test.cpp
|
.txt |
.html |
Tree.vcproj |
Compilación VC++ v7
http://www.di-mare.com/adolfo/p/TreeCpp/Tree_test.vcproj
|
.txt |
.vcproj |
TreeCpp.dxg |
Configuración Doxygen
[v 1.4.5]
http://www.di-mare.com/adolfo/p/TreeCpp/Tree.dxg
|
.txt |
.dxg |
http://www.di-mare.com/adolfo/p/TreeCpp/index.html
http://www.di-mare.com/adolfo/p/TreeCpp/TreeCpp.zip
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
| [-] | Resumen
|
| [1] | Introducción
|
| [2] | El árbol de nodos
|
| [3] | El árbol hecho con base en la lista
|
| [4] | Funcionalidad del árbol
|
| [5] | El concepto de árbol
|
| [6] | Especificación del árbol
|
| [7] | Detalles de implementación
|
| [-] | Conclusión
|
| [-] | Agradecimientos
|
| [-] | Código fuente
|
| |
|
 |
Bibliografía
|
 |
Indice
|
 |
Acerca del autor
|
 |
Acerca de este documento
|
![[/\]](../../img/top.gif)
|
Principio
![[<>]](../../img/index.gif) Indice
Indice
![[\/]](../../img/bottom.gif) Final
Final
|
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
| Adolfo Di Mare: Investigador costarricense en la Escuela de Ciencias de la Computación e Informática [ECCI] de la Universidad de Costa Rica [UCR], en donde ostenta el rango de Profesor Catedrático. Trabaja en las tecnologías de Programación e Internet. También es Catedrático de la Universidad Autónoma de Centro América [UACA]. Obtuvo la Licenciatura en la Universidad de Costa Rica, la Maestría en Ciencias en la Universidad de California, Los Angeles [UCLA], y el Doctorado (Ph.D.) en la Universidad Autónoma de Centro América. |
| Adolfo Di Mare: Costarrican Researcher at the Escuela de Ciencias de la Computación e Informática [ECCI], Universidad de Costa Rica [UCR], where he is full professor and works on Internet and programming technologies. He is Cathedraticum at the Universidad Autónoma de Centro América [UACA]. Obtained the Licenciatura at UCR, and the Master of Science in Computer Science from the University of California, Los Angeles [UCLA], and the Ph.D. at the Universidad Autónoma de Centro América. |
![[mailto]](../../img/mailbox.gif) Adolfo Di Mare <adolfo@di-mare.com>
Adolfo Di Mare <adolfo@di-mare.com>
![[<>]](../../img/index.gif)
![[\/]](../../img/bottom.gif)
![[/\]](../../img/top.gif)
| Referencia: | Di Mare, Adolfo:
Una clase C++ completa para conocer y usar árboles
,
Reporte Técnico ECCI-2005-01,
Escuela de Ciencias de la Computación e Informática,
Universidad de Costa Rica,
http:// www.di-mare.com /adolfo/p/ TreeCpp.htm,
Diciembre 2005.
|
| Internet: |
http://www.di-mare.com/adolfo/p/TreeCpp.htm
http://www.di-mare.com/adolfo/p/TreeCpp.doc
|
| Autor: | Adolfo Di Mare
<adolfo@di-mare.com>
|
| Contacto: | Apdo 4249-1000, San José Costa Rica Tel: (506) 207-4020 Fax: (506) 438-0139 |
| Revisión: | ECCI-UCR, Febrero 2006
|
| Visitantes: |
![[home]](../../img/home.gif) |
![[<>]](../../img/index.gif) |
![[/\]](../../img/top.gif) |